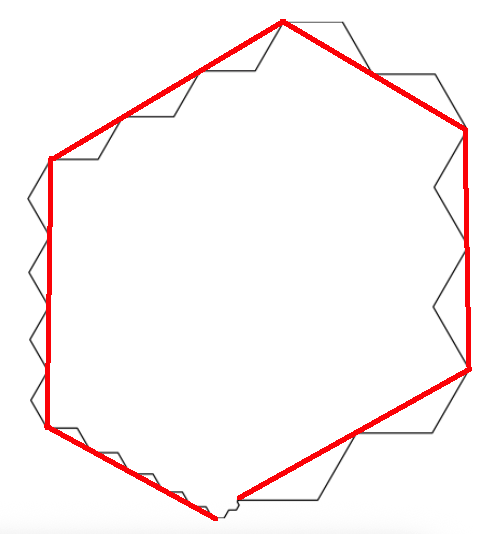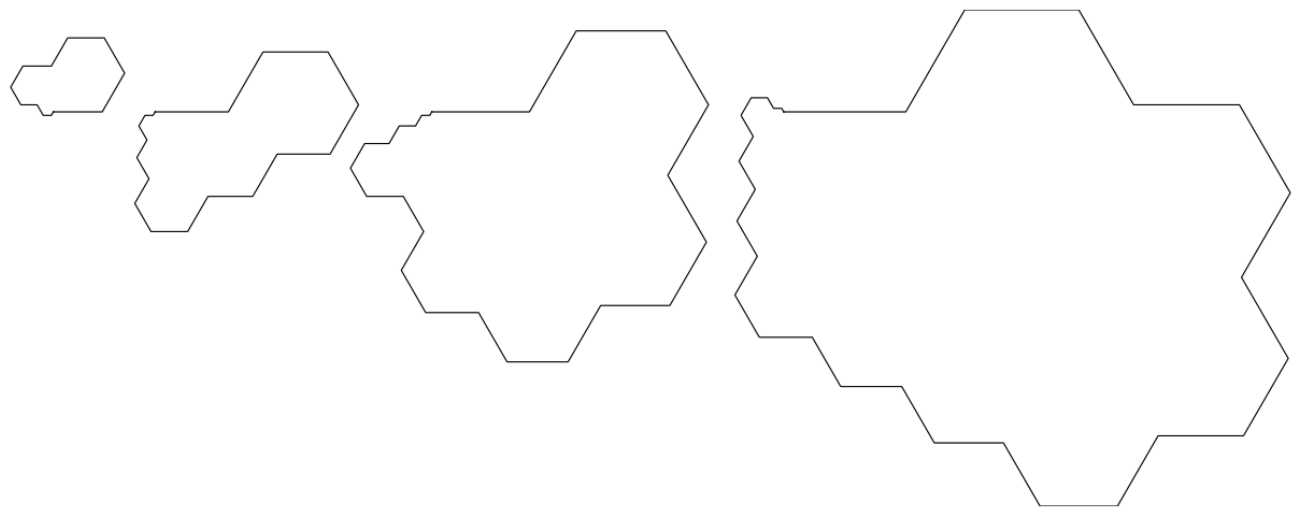
1.attēls: Polimondu piemēri $n=12,18,24,30$.

2.attēls: Polimondu piemēri $n=36,42,48$.

Apgalvojums: Lai eksistētu perfekts platleņķu $n$-polimonds, ir nepieciešami, lai $n \geq 12$ un $n \equiv 0 \pmod{6}$.
Pierādījums: TBD
| n | Skaits |
|---|---|
| 12 | 1 |
| 18 | 1 |
| 24 | 21 |
| 30 | 432 |
| 36 | 13684 |
| 42 | 284674 |
| 48 | 7559582 |
Piezīme: Esam pārliecināti, ka nosacījums ($n \geq 12$ un $n \equiv 0 \pmod{6}$) ir arī pietiekams, lai eksistētu perfekts platleņķu $n$-polimonds. Bet tas būtu jāpamato ar induktīvu konstrukciju vai kādu citu eksistences teorēmu.
Apgalvojums: Ja $n \equiv 0 \pmod{12}$, tad katra perfekta platleņķu polimonda laukums $A$ ir pāra skaitlis, bet ja $n \equiv 6 \pmod{12}$, tad katra perfekta platleņķu $n$-polimonda laukums ir nepāra skaitlis. (Vienības trijstūrīša laukums ir $1$. Tad parastais Eiklīda telpas laukums ir izsakāms kā $A \cdot \frac{\sqrt{3}}{4}$.)
| n | Malas | Laukums |
|---|---|---|
| 12 | ABCDEDEFAFAB | 820 |
| 18 | ABAFEDEDEDCBCBCBAB | 2997 |
| 24 | ABAFEFEDEDCDCBCDCBABABAB | 10178 |
| 30 | ABAFAFEFEDEDCDCDCDCBCBCBCBAFAF | 25617 |
| 36 | ABABCBCDCDCDEDEFEFEFEFEFAFAFAFABABCB | 54692 |
| 42 | ABABCBCBCDCDEDEDEDEFEFEFEFAFAFAFAFAFABABCB | 101621 |
| 48 | ABABCBCDCDCDCDEDEDEFEFEFEFAFAFAFAFAFABABABAFABCB | 170018 |
Hipotēze (par platleņķu polimondu maksimālo laukumu): Ar $A_n$ ($n=12,18,24,30,\ldots$) apzīmēsim lielāko iespējamo perfekta platleņķu polimonda laukumu (mazajam trijstūrītim laukums ir $1$). Ir spēkā
\[\limsup_{n\to\infty} \frac{A_n}{(n^2(n+1)^2)/32} = 1.\]T.i. bezgalīgi bieži vislielākais perfektais platleņķa $n$-polimonds ir ar laukumu, kas asimptotiski tuvojas regulāra sešstūra laukumam, kura malas ir izrobotas tā, ka visi nogriežņi, kas atrodas uz robiņiem veido ar sešstūra malu $30^{\circ}$ leņķi.
Piezīme: Lai uzkonstruētu augošu naturālu skaitļu apakšvirkni $n_1,n_2,\ldots$, kuras locekļi asimptotiski tuvojas sešstūrim, ir nepieciešama induktīva (vai kāda cita) konstrukcija, kura izveido aptuveni vienāda garuma zigzagveida lauztas līnijas, kuras sastāda sešstūri. (Lai figūra būtu noslēgta, var gadīties pievienot vēl arī nedaudzas īsas savienotājmalas pašās beigās.) Ja šāda konstrukcija ir iespējama visiem $n$, kas dalās ar $6$, tad augšējās robežas vietā var pierādīt parastu robežu.